3.1 Temperature¶

https://www.youtube.com/watch?v=o6PHMCpCGj4&list=PLMcpDl1Pr-vjXYLBoIULvlWGlcBNu8Fod&index=22

Overview¶

Chapter 3 has two purposes:

Relate entropy to other quantities.
Use these relations to predict the behavior of the real world.

Background¶

In Chapter 2, we looked at multiplicity and entropy. Entropy is the log of the multiplicity, and the 2nd Law of Thermodynamics states the basic observation that with large enough systems, the multiplicity will increase with such precision that you can’t measure any deviation from the maximum.

Although the 2nd Law is not fundamental, it is going to be treated as if it were.

Temperature¶

We started this textbook with the definition of temperature as “that thing you measure with a thermometer”. Later on, we said that temperature is “that thing that is the same for two bodies in thermal equilibrium.” We didn’t dig very deep into a definition of temperature that didn’t depend on thermometers and physical matter, but now with entropy defined and understood, we can do that. The key connecting fact is that entropy gives us a framework to define what we mean by “thermal equilibrium.”

A Silly Analogy¶

Although Schroeder presents this analogy second, I want to present it first so that the math we are going to do has some sort of context. At the very least, we’re going to need to understand why we’re interested in the partial derivatives of entropy and energy and such, and we want to get an intuitive grasp of what is going on at the atomic level with respect to multiplicity and entropy.

Imagine a world where people are constantly sharing money with each other with the intention of making everyone as happy as possible. People aren’t focused on making themselves as happy as possible, they want to make EVERYONE happy at the same time, or rather, find the combination that will make everyone the happiest, even if it means some people are really happy and others are not. This may mean that everyone gives all their money to a few people, or spread it out equally, or some combination of the above.

The money, in this analogy, are little packets of energy. Since we’re dealing with large enough values, you can consider the money as completely divisible, although we know from quantum mechanics that it is actually made up of tiny units of currency.

The happiness in this example is in fact entropy, or multiplicity. These people are in fact trying to find the greatest multiplicity but they aren’t exactly the brightest people and they can’t exactly see too far in the future. They just know that if they move their money or hold on to it that the total entropy will increase (or decrease) and they let that guide their decision making.

Now, some people are really greedy. They are happiest when they have lots and lots of money. That is to say, they have lots and lots of degrees of freedom and a little bit of energy goes a long way to maximizing entropy. Others are not nearly as greedy, and you might even call them generous. With lots of money, they are not as happy as others. They don’t have as many degrees of freedom and so they really don’t get much happier when you give them more energy.

Now, if you give people more and more money, they start to hit a point where they realize that you’re better off giving the money to someone else who can make more happiness out of it. Even really greedy people eventually begin to “fill up” to the point where giving them more money doesn’t really increase their happiness much anymore. Indeed, they may see someone who has a small amount of money and see that even though they are greedy, just a few dollars will go a long way in making someone else much happier, and so to maximize the total happiness they will gladly impart of some of their money to that person.

This is pretty typical, but some people are really weird. They get even more happy when you give them even more money. (The real-world comparison are things held together with gravity. Adding energy slows them down because their orbits increase, and adding more energy actually increases the entropy per unit energy.)

Temperature, in this scenario, does not correspond, necessarily with energy. It corresponds to their willingness to share. That is, the inverse of whether giving them more energy will increase their entropy or not. If there is diminishing returns, then that means that it is hot. If there is increasing returns, then it is cold.

Keep this analogy in mind as we go through the definition of temperature in the new framework of entropy and multiplicity and such. Keep in mind that we will visit very strange systems that behave very oddly when it comes to entropy. In Figure 3.2 in the book, they have “normal” matter, “miserly” matter and “enlightened” matter that will give some very counter-intuitive results if you think of temperature as being related to energy. However, with the correct intuition of temperature, these systems will make complete sense.

Two Einstein Solids¶

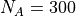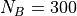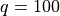Before we go too deep into the math, let’s look at a concrete example. Two Einstein Solids, A and B, are weakly coupled, sharing energy with each other. One has $N_A=300$ and the other $N_B=300$ oscilators (which you can think of as 3 times the number of atoms.) They are sharing between themselves $q=100$ packets of energy.

If we were to graph their entropy vs. energy, we’d see that for each solid, as the energy in that solid increases, their entropy increases – completely expected. Note that there is a slight curve, which is evident near the

There is a maximum 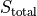$S_\text{total}$ that occurs when 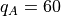$q_A=60$ . We know this is a maximum for two reasons: One, it looks like it. And two, the first partial derivative of the total entropy vs. q_A or q_B is ZERO. That indicates a minimum or a maximum (or a shoulder). We look at the second derivative to tell which way it is pointing, and indeed, the second derivative at that point is negative, so we know we have at least a local maximum.

In math:

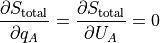
$\frac{\partial S_\text{total}}{\partial q_A} = \frac{\partial S_\text{total}}{\partial U_A} = 0$

We can say the partial of q_A is the partial of U_A because q_A is just the count of energy packets. Multiply by the units, and you have U_A.

Now, we can break up the total entropy into its parts:

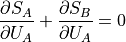
$\frac{\partial S_A}{\partial U_A} + \frac{\partial S_B}{\partial U_A} = 0$

Note that 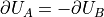$\partial U_A = - \partial U_B$ since when you add energy to A you are removing it from B, and vice-versa.

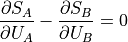
$\frac{\partial S_A}{\partial U_A} - \frac{\partial S_B}{\partial U_B} = 0$

And now we get the elegant-looking:

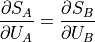
$\frac{\partial S_A}{\partial U_A} = \frac{\partial S_B}{\partial U_B}$

This thing that is equivalent when the total entropy is at its maximum is the partial derivative of the entropy of the part over the energy of the part.

And remember this thing is the temperature? We defined temperature to be that thing that is the same for two bodies after they’ve reached thermal equilibrium, and we’ve decided that thermal equilibrium is reached when entropy is at its maximum, so now we start to have an idea on what temperature is:

$\text{something} = \frac{\partial S}{\partial U}$

Let’s look at this graph some more. Note that that equlibrium, that A would increase in entropy if it had more energy, but B would decrease in entropy if A had more energy, and they have exactly opposite slopes. That is, the slopes are completely balanced. Giving more energy to A or B would not increase the total energy.

In other parts of the graph, the slopes are not opposed. One the left side, if we added more energy to A, the entropy of B would fall a little bit, but the entropy of A would rise rapidly. On the right side, if we added more energy to A, the entropy of A would rise a little bit, but the entropy of B would fall rapidly.

At each point in the graph, the two systems engage in a random process. They offer each other some energy, and whoever would increase more in entropy would get it. When equilibrium is reached, they offer each other a little energy, but decide not to give any away because total entropy would decrease.

This brings us back to the analogy. The reason why A ends up with more energy than B is because it is more greedy than B. A, in more concrete terms, does a better job of putting the energy into more configurations. But if you take away too much energy from B, it is starved for entropy. So A and B are greedy, but they have different levels of greediness depending on how much energy they have. If they have little energy, they really, really want some energy. If they have a lot of energy, adding more doesn’t really do too much to increase entropy.

One final bit: We’d like high temperatures to represent things ready to give away a lot of energy, and low temperatures to represent things ready to consume a lot of energy. That is, greedy things are cold, and generous things are hot.

However, the partial derivative of S over U doesn’t give us that. A big positive number means it’s ready to accept more energy. A small number means it would rather someone else have that energy. So we need to invert it to find the temperature:

$T \equiv \left ( \frac{\partial S}{\partial U} \right )^{-1}_{N,V}$

Note that we’re only looking at how the entropy changes when energy is added (or removed) from it, keeping all other things constant (in particular the number of particules / degrees of freedom and the volume.)

Schroeder points out that you could just flip the partial derivative – how does the energy change with the energy? While this is possible, it is generally not how we think about things, as we expect that S is a reflection of energy, not the other way around.

With this, we can actually calculate the temperatures of these Einstein solids given how much energy is in it. We arrive at about 360 K for A when it is at q_A=13 or 11 units, which is a little bit hot and ready to shed its energy for the sake of the universe entropy increasing. You can calculate if for B with 89 or 87 energy units and see that it is indeed hotter – more willing to give up its energy.

It should now be obvious why entropy has units of J/K.

Problem 3.1¶

Calculate the temperatures.

Problem 3.2¶

Prove the Zeroth Law. Is it trivial? Yes. Is it obvious? Yes. Is it important? Yes.

Problem 3.3¶

It may help to “flip” one of the graphs and look at the sums of the entropies as energy is shared between them. Do this graphically. Just trace the graph on to the back of the page and then through to the front to get a mirror image.

Problem 3.4¶

This one is fun to think about.

Real-World Examples¶

If we take our results from stat mech about Einstein Solids, and plug it in to calculate the temperature:

$\begin{aligned} S &= N k \left [ \ln (q/N) + 1 \right ] \\ &= N k \left [ \ln (U/\epsilon N) + 1 \right ] \\ &= N k \ln U - N k \ln (\epsilon N) + N k \\ \end{aligned}$

Since there’s only one term with a “U” in it, the derivative is simple to calculate:

$T = \left ( \frac{\partial S}{\partial U} \right )^{-1} = \left ( \frac{N k}{U}\right )^-1]$

Which gives us the familiar formula:

$U = NkT$

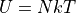
This is the result we obtained earlier using the equipartition theorem. For every oscillator (N is the oscillators, not the atoms), there are 2 degrees of freedom: 1 for the kinetic energy and one for the potential.

Let’s compute the temperature of an ideal gas:

$\begin{aligned} S &= N k \left [ \ln \left ( \frac{V}{N} \left ( \frac{ 4 \pi m U }{ 3N h^2 } \right ) ^{3/2} \right ) + \frac{5}{2} \right ] \\ T &= \left ( \frac{\partial S}{\partial U} \right )^{-1}\\ &= \left ( \frac{\partial}{\partial U} N k \left [ \ln \left ( \frac{V}{N} \left ( \frac{ 4 \pi m U }{ 3N h^2 } \right ) ^{3/2} \right ) + \frac{5}{2} \right ] \right )^{-1}\\ &= \left ( \frac{\partial}{\partial U} \left [ Nk \ln \left ( \frac{V}{N} \right ) + \frac{3}{2} NK \ln \left ( \frac{ 4 \pi m U }{ 3N h^2 } \right ) + \frac{5}{2}NK \right ] \right )^{-1}\\ &= \left ( \frac{\partial}{\partial U} \left [ Nk \ln \left ( \frac{V}{N} \right ) + \frac{3}{2} NK \ln \left ( \frac{ 4 \pi m }{ 3N h^2 } \right ) + \frac{3}{2} NK \ln U + \frac{5}{2}NK \right ] \right )^{-1}\\ &= \left ( \frac{\frac{3}{2}Nk}{U}\right ) ^{-1} \\ U &= \frac{3}{2}NkT \\ \end{aligned}$

This should be no surprise either.

Note that we could start with this and derive the ideal gas law, but that is in Section 3.4 in a more rigorous and general way.

Problem 3.5¶

Find the temperature of a “low temperature” Einstein Solid, where 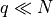$q \ll N$ . Not much to say here, except it’s all math.

Problem 3.6¶

Find the temperature of anything that follows the equipartition theorem, and then comment on what happens at low temperatures.

Problem 3.7¶

Calculating the temperature of a black hole, and then looking at how the entropy behaves according to energy, and we get some interesting results. Stay away from black holes, please.

Patreon Supporters¶

Tony Ly is our first $20/month supporter. My eternal gratitude for his pledge.

You can support me via Patreon, or by buying textbooks through my Amazon affiliates link. To be honest, what I need most is to get my channel shared with your friends. YouTube is kind of weird in how it recommends videos and channels, and so a lot of good creators are just hidden because YouTube doesn’t know that we want to see them.